Archimedes and the area of sphere

Posted on 05/01/2018 by KKK

I record here a remarkable discovery of Archimedes about the formula for the surface area of a sphere. I think the derivation is elementary enough so that it can be taught in high school. (I think I was not taught any derivation of it the first time I learned it, but I derived it myself after learning enough calculus.) The sad thing about our math education is that we are fed with tons of formulas, often without much motivation, that even the good students have to resort to mere memorization. My point is that many formulas taught in high school can be demonstrated in a rather natural and elementary way, which can be helpful to understand or remember them.

About 1800 years prior to the discovery of calculus, Archimedes showed that the surface area of a sphere of radius {r} is {4\pi r^2}. He also showed that the volume of a ball of radius {r} is {\frac{4}{3}\pi r^3} using the Cavalieri’s principle, again without calculus (this is explained in the last part of my calculus notes here).

450px-Domenico-Fetti_Archimedes_1620

Archimedes (287 –  212 BC)

Let us now describe how he discovered the surface area of a sphere. First, we inscribe the sphere of radius {r} in a cylinder of the same radius and height {2r} as shown.

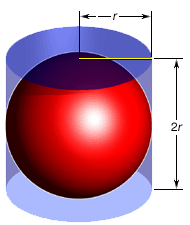
inscribedsphere

We claim that the orthogonal projection from the lateral face of the cylinder onto the sphere is area-preserving. This of course can be shown by calculus. Remarkably, Archimedes proved it without using calculus. Unavoidably, this would not be completely rigorous in today’s standard as we lack the precise definition of area if we avoid calculus, and have to resort to the language of the “infinitesimals”.

The following picture is the cross section of the inscribed sphere along the {x-z} plane, which then becomes a circle of radius {r} inscribed in a square of side {2r}.

archsphere2


Suppose {\Delta \theta} is the “infinitesimal” increment of the angle {\theta}. Then on one hand (if we ignore the {\pm} sign),

\displaystyle \begin{array}{rl} \displaystyle \Delta z=r \Delta \theta \cos \left(\frac{\pi}{2}-\theta\right)=r\Delta \theta \sin \theta. \ \ \ \ \ (1)\end{array}

So the infinitesimal area element of the cylinder is

\displaystyle \begin{array}{rl} \displaystyle \Delta A_{\mathrm{cylinder}} =& \displaystyle 2\pi r \cdot \Delta z\\ =& \displaystyle 2\pi r ^2 \sin \theta \Delta \theta. \end{array}

On the other hand, the infinitesimal area element of the sphere (the area corresponding to the projection of \Delta A_{\mathrm{cylinder}}) is (see Fig. 1)

\displaystyle \begin{array}{rl} \displaystyle \Delta A_{\mathrm{sphere}} =& \displaystyle r \Delta \theta\cdot 2\pi r \sin \theta\\ =& \displaystyle 2\pi r^2 \sin \theta\Delta \theta\\=&\displaystyle \Delta A_{\mathrm{cylinder}}. \end{array}

We conclude that the projection is area-preserving and so the lateral face of the cylinder has the same area as the sphere. So the sphere has area {2\pi r\times 2r=4\pi r^2}.

Exercise: Make the above argument precise by using the language of differential forms. For example, as {z=r\cos \theta}, we have {dz=-r\sin \theta d\theta}, which (up to a sign) is the rigorous version of (1).

This entry was posted in Calculus, Geometry. Bookmark the permalink.

Leave a comment