Archimedes’ principle for hyperbolic plane

Posted on 06/01/2018 by KKK

After writing the previous post, I realized that there is an exact analogue of the Archimedes’ principle for the surface area of the hyperbolic disk inside the hyperbolic plane.

450px-Domenico-Fetti_Archimedes_1620

Archimedes (287 –  212 BC)


Let us fix the notations. Let {\mathbb R^{2,1}} be the {3}-dimensional Minkowski space defined by

\displaystyle \begin{array}{rl} \displaystyle \mathbb R^{2,1}:=\{(x, y, t)\in \mathbb R^{3}\}, \end{array}

equipped with the Lorentzian metric {-dt^2+dx^2+dy^2}.

Fix {r >0} and define the hyperbolic plane {\mathbb H^2(r)} by

\displaystyle \begin{array}{rl} \displaystyle \mathbb H^2(r):=\{(x, y, t)\in \mathbb R^{2,1}: \quad t>0,\quad t^2-x^2-y^2=r^2\}, \end{array}

equipped with the induced metric.

hyperboloid2

Hyperbolic plane

It can be shown that {\mathbb H^2(r)} is a surface with constant curvature {-\frac{1}{r^2}} (analogous to the fact that the sphere of radius {r}, {\mathbb S^2(r)}, is a surface with constant curvature {\frac{1}{r^2}}). It is easy to see that {\mathbb H^2(r)} can be parametrized by

\displaystyle \begin{array}{rl} \displaystyle X(\theta, \phi)= (r\sinh \theta \cos \phi,r \sinh \theta \sin \phi, r\cosh \theta), \quad \theta\ge 0, \quad \phi\in[0, 2\pi],\end{array}

the “polar coordinates” around {P=(0, 0, r)}, with {r\theta} being the (geodesic) distance from {P}.

Finally, let the (infinite) cylinder {C} of radius {r} be defined by

\displaystyle \begin{array}{rl} \displaystyle C= \{(x, y, t)\in \mathbb R^{2,1}: x^2+y^2=r^2\}, \end{array}

again equipped with the induced metric.

cylinder.png

Cylinder

There is a natural orthogonal projection {\Pi} from {\mathbb H^2(r)\setminus \{P\}} to {C} defined by

\displaystyle \begin{array}{rl} \displaystyle \Pi(x, y, t)=\left(\frac{r x}{\sqrt{x^2+y^2}}, \frac{r y}{\sqrt{x^2+y^2}}, t\right). \end{array}

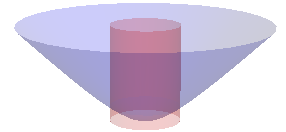
cylin_hyp

The natural projection

In polar coordintes, this is given by

\displaystyle \begin{array}{rl} \displaystyle \Pi(X(\theta, \phi ))=(r\cos \phi, r\sin \phi, r\cosh \theta). \ \ \ \ \ (1)\end{array}

We claim that the map {\Pi} is area-preserving. If this is true, then we can easily calculate the area of the hyperbolic geodesic disk (with radius {rR})

\displaystyle \begin{array}{rl} \displaystyle B_R:=\{X(\theta, \phi): 0\le \theta\le R\}\end{array}

because the projection of {B_R\setminus \{P\}} is exactly the finite cylinder

\displaystyle \begin{array}{rl} \displaystyle \Pi(B_R\setminus \{P\})=\{(x, y, t)\in C: r<t\le r\cosh R\} \end{array}

whose area is easy to be calculated. Indeed, the area of the cylinder is exactly the same as the ordinary cylinder in the Euclidean space {\mathbb R^3}.

hyp_ball

A geodesic disk inside the hyperbolic plane

Now, it is easy to see that in the coordinates {(\theta, \phi)}, the area form of {\mathbb H^2(r)} is given by

\displaystyle \begin{array}{rl} \displaystyle \omega_{\mathbb H^2(r)}= r^2\sinh \theta d\theta\wedge d\phi. \ \ \ \ \ (2)\end{array}

On the other hand, the area form of the cylinder is given by

\displaystyle \begin{array}{rl} \displaystyle \omega_{C}=rdt\wedge d\phi \ \ \ \ \ (3)\end{array}

if {C} is parametrized by {(r\cos \phi, r\sin \phi, t)}.

From (1) and (3), we see that (note that {d\phi(-r \sin \phi, r\cos \phi, 0)=1})

\displaystyle \begin{array}{rl} \displaystyle \omega_C(d \Pi(X_\theta), d\Pi(X_\phi))=r^2\sinh\theta. \end{array}

Comparing with (2), we conclude that {\Pi^*\omega_C=\omega_{\mathbb H^2(r)}}, i.e. {\Pi} is area-preserving. As a corollary, we get

Corollary 1 The area of {B_R} is

\displaystyle \begin{array}{rl} \displaystyle \mathrm{Area}(B_R)=2\pi r^2(\cosh R-1). \end{array}

This entry was posted in Calculus, Differential geometry, Geometry. Bookmark the permalink.

Leave a comment