Sobolev and Isoperimetric Inequality

Posted on 06/10/2013 by KKK

In this short note I will prove the equivalence of the Sobolev inequality and the isoperimetric inequality. The material here is somewhat standard, and this note is mostly for my own benefit.

Let {(M,g)} be an n-dimensional Riemannian manifold, n\ge 2. The isoperimetric property (or more commonly, isoperimetric inequality) states that there exists a constant {C} such that for any relatively compact domain {\Omega} with smooth boundary, we have

\displaystyle C\mathrm{Vol}(\Omega)^{\frac{n-1}{n}}\le \mathrm{Area}(\partial \Omega). \ \ \ \ \ (1)

The Sobolev inequality states that on a compact n-dimensional Riemannian manifold {(M,g)} (possibly with boundary), there exists a constant {C} (different from that in (1)) such that

\displaystyle C(\int_M |f|^{\frac{n}{n-1}})^{\frac{n-1}{n}}\le \int_M |\nabla f|, \ \ \ \ \ (2)

provided that {\int_M f =0} if {\partial M=\emptyset}; otherwise we assume either {\int_M f =0} or {f\in W^{1,2}_0} (the completion of {C_c^\infty} under the norm {\|f\|^2=\int_M (|f|^2 +|\nabla f|^2) }).

It is well-known that for a non-compact Riemannian manifold, the Sobolev inequality and the isoperimetric property may fail.

For example, let {M} be the surface obtained by revolving the graph of {1/x} about the {x}-axis. Then {M} has a “cusp end” which has infinite area. On the other hand, for any {A>0}, we can choose {\Omega} whose boundary consists of two circles of arbitrary small length on the cusp, such that the area of {\Omega} is {A}. Therefore {M} does not have the isoperimetric property. By suitably choosing {f} to be a “bump function” on this {\Omega}, we can also see that the Sobolev inequality fails to hold on {M} .

surface with a cusp
The surface M does not satisfy the isoperimetric property.

In this short note, we prove the following: for a general Riemannian manifold (in particular, non-compact), the isoperimetric property is equivalent to the Sobolev inequality.
Proof: Let us assume the Sobolev inequality. For {\varepsilon>0}, we define the function

\displaystyle f_\varepsilon(x)= \begin{cases} 1, &\quad x\in \Omega, d(x, \partial \Omega)\ge \varepsilon,\\ \frac{d(x, \partial \Omega)}{\varepsilon}, &\quad x\in \Omega, d(x, \partial \Omega)\le \varepsilon,\\ 0, &\quad x\not\in \Omega. \end{cases}

Apply the Sobolev inequality (2) to {f_\varepsilon}, and take {\varepsilon\rightarrow 0}, we can get the isoperimetric property (1).

Now we prove the converse. We can without loss of generality assume {f\ge 0}. By the layercake integral formula, we have

\displaystyle \begin{array}{rl} \int_M |f|^{\frac{n}{n-1}} =&\int_0^\infty \mathrm{Vol}(f^{\frac{n}{n-1}}\ge t)dt\\ =&\int_0^\infty \mathrm{Vol}(f\ge t^{\frac{n-1}{n}})dt\\ =&\frac{n}{n-1}\int_0^\infty \mathrm{Vol}(f\ge s)s^{\frac{1}{n-1}}ds. \end{array}

On the other hand, by the coarea formula and the isoperimetric inequality (1),

\displaystyle \begin{array}{rl} \int_M |\nabla f| =&\int_0^\infty \mathrm{Area}(f=s)ds\\ \ge&C_1\int_0^\infty\mathrm{Vol}(f\ge s)^{\frac{n-1}{n}}ds \end{array}

So to prove (2), it suffices to show that

\displaystyle \left(\int_0^\infty \mathrm{Vol}(f\ge s)^{\frac{n-1}{n}}\right)^{\frac{n}{n-1}}\ge C_2 \int_0^\infty \mathrm{Vol}(f\ge s)s^{\frac{1}{n-1}}ds.

Putting {f=1} suggests that {C_2= \frac{n}{n-1}} (though strictly speaking, such {f} may not be admissible for the Sobolev inequality; nevertheless we can get around this problem by modifying {f} to be a smooth bump function with range {[0,1]} supported on a compact region, similar to {f_\varepsilon} above). Therefore, if we let {V(s)= \mathrm{Vol}(f\ge s)}, then we have to show that

\displaystyle \left(\int_0^\infty V(s)^{\frac{n-1}{n}}ds\right)^{\frac{n}{n-1}}\ge \frac{n}{n-1}\int_0^\infty V(s)s^{\frac{1}{n-1}}. \ \ \ \ \ (3)

Let

\displaystyle f_1(t)= \left(\int_0^tV(s)^{\frac{n-1}{n}}ds\right)^{\frac{n}{n-1}}\quad \mathrm{and}\quad f_2(t)=\frac{n}{n-1}\int_0^t V(s)s^{\frac{1}{n-1}}.

We want to show that {f_1(t)\ge f_2(t)}. Clearly, {f_1(0)=f_2(0)=0}. By direct computation, {f_1'(t)\ge f_2'(t)} if and only if

\displaystyle \begin{array}{rl} \int_0^t V(s)^{\frac{n-1}{n}}ds \ge V(t)^{\frac{n-1}{n}}t. \end{array}

But this follows directly from the monotone decreasing property of {V(s)} (clearly {V} is non-increasing):

\displaystyle \int_0^ t V(s)^{\frac{n-1}{n}}ds\ge \int_0^t V(t)^{\frac{n-1}{n}}ds= V(t)^{\frac{n-1}{n}}t.

Thus {f_1(t)\ge f_2(t)} and so putting {t=\infty}, we conclude that (3) is true. This completes the proof.

\Box

This entry was posted in Geometry, Inequalities. Bookmark the permalink.

4 Responses to Sobolev and Isoperimetric Inequality

  1. Anonymous says:
    30/03/2017 at 10:38 pm

    how can one soblev inequality to the function {f_\epsilon},

    Reply
  2. KKK says:
    10/04/2017 at 7:00 pm

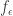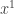    Whether f_\epsilon is weakly differentiable is a local issue. At any point p on the boundary \partial \Omega, we can choose a local coordinates such that p is mapped to 0, x^1>0 corresponds to \Omega and the x^1-curves corresponds to the geodesics normal to \partial \Omega. Under this coordinates, the corresponding function is then
    \displaystyle \begin{array}{rl} \displaystyle f_\varepsilon(x)= \begin{cases} 1, & \displaystyle \quad x^1\ge \varepsilon,\\ \frac{x^1}{\varepsilon}, & \displaystyle \quad 0<x^1\le \varepsilon,\\ 0, & \displaystyle \quad x\le 0. \end{cases} \end{array}
    This function is easily seen to be weakly differentiable, and the weak derivative is zero for x^1>\varepsilon and x^1<0.

    Reply
  3. A says:
    19/07/2018 at 8:25 pm

    In the first part, why do we have $\int |\nabla f_\epsilon| \to |\partial \Omega|$?

    Reply

Leave a comment